The Challenge

A working knowledge of basic mathematics empowers individuals to engage productively in a society and economy that increasingly rely on data and quantitative reasoning. Yet all too often, mathematics is an obstacle, rather than an opportunity, to students who want to achieve their career goals through higher education.

student barriers image

Traditional entry–level college mathematics programs fail to serve students well because they are structured as disconnected courses whose content is misaligned to students’ career and life needs, and inconsistent math requirements across institutions create barriers for transfer. Underprepared students are especially impacted by multi–semester, “developmental” course sequences, and, very often, are assessed as underprepared using inappropriate placement practices or instruments. These long sequences underestimate students’ capability to learn mathematics and delay students’ engagement with the college–level coursework that is required for their degree programs. Minority and underserved populations are disproportionately impacted by these problems.

LEARN MORE: Read The Case for Mathematics Pathwaysview full resourceView Full ResourceDownloadFile

 

Where Is the Evidence?

Expand this section to find out.

 

The mismatch of mathematics content to students’ needs is evidenced by the fact that College Algebra was designed as a preparation for Calculus, yet only as few as 10% of students in College Algebra take Calculus.1 Students who are successful in passing classes do not learn skills and concepts that will be useful to them. Many others fail the courses in part because students are less motivated to learn material when they do not see how it connects to their lives. In A Common Vision for Undergraduate Mathematical Sciences Programs in 2025, five major mathematical professional associations called “for multiple pathways into and through mathematical sciences curricula, some of which should include early exposure to statistics, modeling, and computation.”2

The negative impact of long developmental course sequences on student success is documented in multiple large–scale studies including a Community College Research Center study that found only 20% of students enrolled in developmental mathematics earned college math credit in three years or less.3

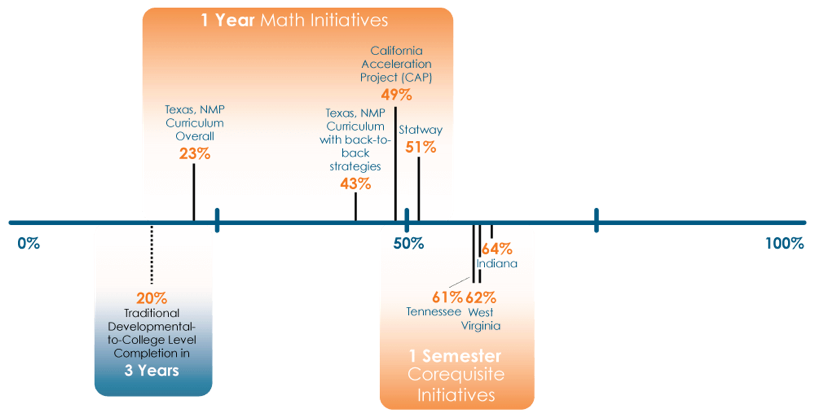
co-requisite image_learn About page_resource site_0.png

 

Although the data are dismal, there is great hope in the growing evidence that many underprepared students can be successful in gateway mathematics courses aligned to their programs of study if they are provided well-designed co-requisite supports. As shown here, a number of programs have helped underprepared students succeed in college–level math courses at higher rates and in less time compared to the traditional developmental sequences.4 Most stunning, the highest rates of success have come from one–semester co–requisite models. Further, when one–year models are appropriate, their success is greatly increased when the first and second semesters are linked through what the Dana Center refers to as strategies for continuous enrollment in mathematics course sequences.

1 Dunbar, S. R. (2005). Enrollment flow to and from courses below calculus. In N. B. Hastings (Ed.), A fresh start for collegiate mathematics: Rethinking the courses below calculus. Washington DC: Mathematical Association of America.

2 Page 13 in Saxe, K., & Braddy, L. (2015). A common vision for undergraduate mathematical sciences programs in 2025. Washington, DC: The Mathematical Association of America.

3 Bailey, T., Jeong, D. W., & Cho, S. (2009). Referral, enrollment, and completion in developmental education sequences in community colleges. (CCRC Working Paper No. 15). New York: Community College Research Center, Teachers College.

4 California Acceleration Project. (2015). Acceleration strategies that produce powerful results: A planning resource for community colleges.

  Rutschow, E. Z., & Diamond, J. (2015, April). Laying the foundations: Early findings from the New Mathways Project. New York: MDRC.

beige
Uri Treisman
“The true power in math pathways work is not in any discrete strategy or course multiplied by a factor of n; it’s in the connections within and across programs, institutions, and sectors that effect systemic and sustainable change.”
Uri Treisman, Ph.D., | University Distinguished Teaching Professor | Professor of Mathematics, Professor of Public Affairs | Executive Director, The Charles A. Dana Center at The University of Texas at Austin
Math Pathways as a Solution

Simply put, math pathways are a course or sequence of courses a student takes to meet the requirements of his or her program. These pathways should be designed to align with students’ career and life needs, and should accelerate underprepared students’ entry into credit–bearing coursework.

The Dana Center advocates for pathways designed in accordance with four principles, which we collectively refer to as the DCMP model. The first two principles are structural changes, and the second two principles are continuous improvements.

 

Institutions implement structural and policy changes quickly and at scale.

Mathematics pathways are structured so that:

PRINCIPLE 1: All students, regardless of college readiness, enter directly into mathematics pathways aligned to their programs of study.

PRINCIPLE 2: Students complete their first college–level math requirement in their first year of college.

 

Institutions and departments engage in a deliberate and thoughtful process of continuous improvement to ensure high–quality, effective instruction.

Students engage in a high–quality learning experience in mathematics pathways that are designed so that:

PRINCIPLE 3: Strategies to support students as learners are integrated into courses and are aligned across the institution.

PRINCIPLE 4: Instruction incorporates evidence–based curriculum and pedagogy.

LEARN MORE: Read about the DCMP model and what enactment of each principle entails.

beige

Join the Joyful Conspiracy

Making mathematics pathways the normative practice at full scale within and across institutions requires coordinated actions across stakeholder groups and across sectors. Uri Treisman coined the phrase “the Joyful Conspiracy” to describe this united effort.

Explore the critical roles of each stakeholder group:

POLICY INSTITUTIONAL LEADERSHIP 

MATH FACULTY PARTNER DISCIPLINES 

ADVISORS AND COORDINATORS

white